[C++]型だけでN bit加算器を書こう

2021.06.17に公開

最近、Twitter で以下の記事を見かけました。

https://qiita.com/Kuniwak/items/983ba68fcf68d915b07d

2018 年の記事と少し古めですが、TypeScript の型システムを利用して論理ゲート～ 4bit 加算器を実装しています。こんなものを見かけたら、C++でもやりたくなってしまうのが人間というものです。ということなので、今回は C++の型システムで組み合わせ回路を実装していきたいと思います。やりたかっただけです。

レギュレーション

上記の記事では、TypeScript の型システムを用いた静的計算を「コンパイル時計算」とし、TypeScript のコンパイル時計算で組み合わせ回路を実装するという趣旨になっていました。しかし、C++でこの言葉をそのまま採用して実装すると、constexprで世界のすべてを殴り倒すことが出来てしまい、面白くありません。せっかくなので今回は、以下のような条件のもとでコードを書いてみましょう。

非型テンプレートパラメータ以外の場所では、定数値を含め値を書かない。
同様に、非型テンプレートパラメータを算出する以外の目的でconstexprな処理を利用しない。
実行時の処理については、上記の制約の対象としない。ただし、実行時にして良い処理は入出力に関するもののみとする。

もはや型で遊びたいだけであり、何が目的の実装なのかよくわかりませんが(そもそもレギュレーションガバガバですが)、まあよいでしょう。

検証環境

clang version 12.0.0
x86_64-pc-linux-gnu
std=c++2a

注意点

本記事の実装では、fold expression の展開数制限および template の再帰深度上限を回避するような実装は行っていません。ですので、N を大きくしていくと意外とすぐ死にます。

バイナリ型を定義する

先駆者様に倣って、0 or 1 の保持にも型を利用していこうと思います。ここは複雑ではありませんので、全体のコードをいきなり提示します。

binary.h

#pragma once
#include <type_traits>

namespace Binary {
    struct Binary {};
    struct I : public Binary {};
    struct O : public Binary  {};

    template <typename T>
    concept IsBinary = std::is_base_of_v<Binary, T>;

    template <typename T>
    concept IsZero = std::is_same_v<T, O> && IsBinary<T>;

    template <typename T>
    concept IsOne = std::is_same_v<T, I> && IsBinary<T>;
}

マーカーの役割を果たすBinary型と、それを継承したOとIのバイナリ型を定義しました。今回はドントケアを含む回路は想定しませんので、回路で現れる値(型だけど)が 0 と 1 以外の値を取ることはありません。ですので、渡されてきた型がバイナリであるか、つまりOとIのどちらかであるかを判断するコンセプトを定義しています。また、対象の型がOであるか、Iであるかを判断するためのIsZeroとIsOneのコンセプトも用意しました。

最低限の出力処理を用意しておく

この後論理ゲートを実装していきますが、結果が確認できないと困ります。予め最低限の出力処理を用意しておくことにします。レギュレーションより、ここでは自由な値の利用が許可されます。

最低限の出力処理

using Binary::O;
using Binary::I;

template <Binary::IsBinary T>
struct bitToChar {};

template <Binary::IsZero T>
struct bitToChar<T> { inline static constexpr const char v = '0'; };

template <Binary::IsOne T>
struct bitToChar<T> { inline static constexpr const char v = '1'; };

template <Binary::IsBinary T>
constexpr const char bitToCharV = bitToChar<T>::v;

template <template <typename, typename> typename Gate>
static void printTruthTable() {
    fmt::print("0 0 | {}\n", bitToCharV<Gate<O, O>>);
    fmt::print("0 1 | {}\n", bitToCharV<Gate<O, I>>);
    fmt::print("1 0 | {}\n", bitToCharV<Gate<I, O>>);
    fmt::print("1 1 | {}\n", bitToCharV<Gate<I, I>>);
}

このコードは、2 入力 1 出力のゲート型を受け取って、その真理値表を出力するものです。基本論理ゲートの動作確認にはこれを使っていきます。

基本論理ゲートを実装する

前述の記事では、基本論理ゲートの出力をテーブル化して参照するようにしていました。しかし、NAND 論理の完全性を利用すれば NAND 以外のゲートをテーブル化する必要はありませんので、本記事ではテーブル化するゲートは NAND のみとし、その他のゲートは NAND 型を組み合わせた型として実装していきます。

NAND ゲート型

NAND ゲートの実装は以下のようなものにしました。

basic_gates.h(NAND部)

    template <Binary::IsBinary A, Binary::IsBinary B>
    struct NAND  {};
    template <Binary::IsZero A, Binary::IsZero B>
    struct NAND<A, B>  { using X = Binary::One; };
    template <Binary::IsZero A, Binary::IsOne B>
    struct NAND<A, B>  { using X = Binary::One; };
    template <Binary::IsOne A, Binary::IsZero B>
    struct NAND<A, B>  { using X = Binary::One; };
    template <Binary::IsOne A, Binary::IsOne B>
    struct NAND<A, B>  { using X = Binary::Zero; };
    template <Binary::IsBinary A, Binary::IsBinary B>
    using NANDv = typename NAND<A, B>::X

C++20 のコンセプト万々歳です。とても楽にテンプレートパラメータに基づいたオーバーロードを書くことが出来ます。これで、NAND 型のテンプレートパラメータとして渡された 2 つのバイナリ型の組み合わせによって、NAND 型がその内部に NAND ゲートの出力であるバイナリ型の型エイリアスXを持つようになります。

動作しているかどうか、先程用意した出力処理を利用して検証してみます。

NAND出力テスト

int main()
{
    printTruthTable<Gates::NANDv>();
}

出力

どうやらしっかり動作しているようです！

その他のゲートの型を用意する

先述したとおり、あらゆる論理ゲートは NAND ゲートを用いて表現することが出来ます。つまりは、NAND 型を組み合わせるだけで他のゲートの型は用意できるわけです。一気にやってしまいましょう。

basic_gates.h(その他のゲート達)

    template <Binary::IsBinary A>
    using NOT = NAND<A, A>;
    template <Binary::IsBinary A>
    using NOTv = typename NOT<A>::X;

    template <Binary::IsBinary A, Binary::IsBinary B>
    using AND = NOT<NANDv<A, B>>;
    template <Binary::IsBinary A, Binary::IsBinary B>
    using ANDv = typename AND<A, B>::X;

    template <Binary::IsBinary A, Binary::IsBinary B>
    using OR = NAND<NOTv<A>, NOTv<B>>;
    template <Binary::IsBinary A, Binary::IsBinary B>
    using ORv = typename OR<A, B>::X;

    template <Binary::IsBinary A, Binary::IsBinary B>
    using NOR = NOT<ORv<A, B>>;
    template <Binary::IsBinary A, Binary::IsBinary B>
    using NORv = typename NOR<A, B>::X;

    template <Binary::IsBinary A, Binary::IsBinary B>
    using XOR = NAND<NANDv<A, NANDv<A, B>>, NANDv<NANDv<A, B>, B>>;
    template <Binary::IsBinary A, Binary::IsBinary B>
    using XORv = typename XOR<A, B>::X

NOT/AND/OR/NOR/XORの型を定義しました。すべてエイリアステンプレートのみによって実現することが出来ました。NANDに感謝です。

一応、出力を確認しておきましょう。

出力テスト

int main()
{
    printTruthTable<Gates::ANDv>("NAND");
    printTruthTable<Gates::ORv>("OR");
    printTruthTable<Gates::NORv>("NOR");
    printTruthTable<Gates::XORv>("XOR");
}

[NAND]
0 0 | 0
0 1 | 0
1 0 | 0
1 1 | 1
[OR]
0 0 | 0
0 1 | 1
1 0 | 1
1 1 | 1
[NOR]
0 0 | 1
0 1 | 0
1 0 | 0
1 1 | 0
[XOR]
0 0 | 0
0 1 | 1
1 0 | 1
1 1 | 0

完璧です。きちんと型のみで論理ゲートが実装できています。

基本論理ゲートのソースコード

基本論理ゲートの実装全体を以下に示しておきます。

basic_gates.h

#pragma once

#include "binary.h"

namespace Gates {
    template <Binary::IsBinary A, Binary::IsBinary B>
    struct NAND  {};
    template <Binary::IsZero A, Binary::IsZero B>
    struct NAND<A, B>  { using X = Binary::I; };
    template <Binary::IsZero A, Binary::IsOne B>
    struct NAND<A, B>  { using X = Binary::I; };
    template <Binary::IsOne A, Binary::IsZero B>
    struct NAND<A, B>  { using X = Binary::I; };
    template <Binary::IsOne A, Binary::IsOne B>
    struct NAND<A, B>  { using X = Binary::O; };
    template <Binary::IsBinary A, Binary::IsBinary B>
    using NANDv = typename NAND<A, B>::X;

    template <Binary::IsBinary A>
    using NOT = NAND<A, A>;
    template <Binary::IsBinary A>
    using NOTv = typename NOT<A>::X;

    template <Binary::IsBinary A, Binary::IsBinary B>
    using AND = NOT<NANDv<A, B>>;
    template <Binary::IsBinary A, Binary::IsBinary B>
    using ANDv = typename AND<A, B>::X;

    template <Binary::IsBinary A, Binary::IsBinary B>
    using OR = NAND<NOTv<A>, NOTv<B>>;
    template <Binary::IsBinary A, Binary::IsBinary B>
    using ORv = typename OR<A, B>::X;

    template <Binary::IsBinary A, Binary::IsBinary B>
    using NOR = NOT<ORv<A, B>>;
    template <Binary::IsBinary A, Binary::IsBinary B>
    using NORv = typename NOR<A, B>::X;

    template <Binary::IsBinary A, Binary::IsBinary B>
    using XOR = NAND<NANDv<A, NANDv<A, B>>, NANDv<NANDv<A, B>, B>>;
    template <Binary::IsBinary A, Binary::IsBinary B>
    using XORv = typename XOR<A, B>::X;
}

ここまでくれば加算器なんて簡単です。

加算器

型で加算器を実装していきます。

半加算器

全加算器を作るためには、まず半加算器からです。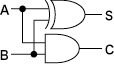半加算器は出力が複数あるため、これまでのように基本論理ゲートのエイリアステンプレートで定義することは出来ません。構造体を使って独自の型として実現していきましょう。

basic_adders.h(HalfAdder部)

    template <Binary::IsBinary A, Binary::IsBinary B>
    struct HalfAdder {
        using X = Gates::XORv<A, B>;
        using Y = Gates::ANDv<A, B>;
    };

以上です。なんと容易いのでしょうか。XORが既に存在するおかげで、半加算器はたったこれだけのコードで実現できました。動作を確認します。出力が増えたため、新たな出力関数を定義しています。

出力テスト

template <template <typename, typename> typename Gate>
static void printTruthTable2_2(const std::string& title) {
    fmt::print("[{}]\n", title);
    fmt::print("A B | Y X\n", title);
    fmt::print("0 0 | {} {}\n", bitToCharV<typename Gate<O, O>::Y>, bitToCharV<typename Gate<O, O>::X>);
    fmt::print("0 1 | {} {}\n", bitToCharV<typename Gate<O, I>::Y>, bitToCharV<typename Gate<O, I>::X>);
    fmt::print("1 0 | {} {}\n", bitToCharV<typename Gate<I, O>::Y>, bitToCharV<typename Gate<I, O>::X>);
    fmt::print("1 1 | {} {}\n", bitToCharV<typename Gate<I, I>::Y>, bitToCharV<typename Gate<I, I>::X>);
}

int main()
{
    printTruthTable2_2<Circuits::HalfAdder>("HalfAdder");
}

[HalfAdder]
A B | Y X
0 0 | 0 0
0 1 | 0 1
1 0 | 0 1
1 1 | 1 0

きちんと加算できていますし、桁上りの出力も正常です。半加算器型が実現できています。

全加算器

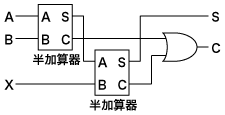半加算器と全く同じです。違いを上げるとすれば、可読性のために構造体内部で型エイリアスを利用しているくらいです。

basic_adders.h(FullAdder部)

    template <Binary::IsBinary A, Binary::IsBinary B, Binary::IsBinary C>
    class FullAdder {
        using HA1 = HalfAdder<A, B>;
        using HA2 = HalfAdder<typename HA1::X, C>;
    public:
        using X = typename HA2::X;
        using Y = Gates::ORv<typename HA1::Y, typename HA2::Y>;
    };

早速出力を見てみましょう。今度は入力が増えたので、再び新たな出力関数を定義しています。

出力テスト

template <template <typename, typename, typename> typename Gate>
void printTruthTable3_2(const std::string& title)
{
    fmt::print("[{}]\n", title);
    fmt::print("A B C | Y X\n"
               "0 0 0 | {} {}\n0 0 1 | {} {}\n0 1 0 | {} {}\n0 1 1 | {} {}\n"
               "1 0 0 | {} {}\n1 0 1 | {} {}\n1 1 0 | {} {}\n1 1 1 | {} {}\n",
            bitToCharV<typename Gate<O, O, O>::Y>,
            bitToCharV<typename Gate<O, O, O>::X>,
            bitToCharV<typename Gate<O, O, I>::Y>,
            bitToCharV<typename Gate<O, O, I>::X>,
            bitToCharV<typename Gate<O, I, O>::Y>,
            bitToCharV<typename Gate<O, I, O>::X>,
            bitToCharV<typename Gate<O, I, I>::Y>,
            bitToCharV<typename Gate<O, I, I>::X>,
            bitToCharV<typename Gate<I, O, O>::Y>,
            bitToCharV<typename Gate<I, O, O>::X>,
            bitToCharV<typename Gate<I, O, I>::Y>,
            bitToCharV<typename Gate<I, O, I>::X>,
            bitToCharV<typename Gate<I, I, O>::Y>,
            bitToCharV<typename Gate<I, I, O>::X>,
            bitToCharV<typename Gate<I, I, I>::Y>,
            bitToCharV<typename Gate<I, I, I>::X>
            );
}

int main()
{
    printTruthTable3_2<Circuits::FullAdder>("FullAdder");
}

[FullAdder]
A B C | Y X
0 0 0 | 0 0
0 0 1 | 0 1
0 1 0 | 0 1
0 1 1 | 1 0
1 0 0 | 0 1
1 0 1 | 1 0
1 1 0 | 1 0
1 1 1 | 1 1

はい。完璧です。

N bit 加算器

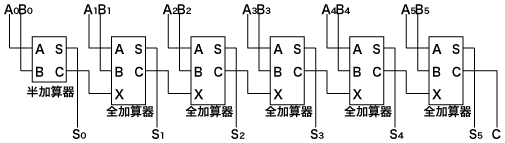さて、全加算器が出来ましたので、複数 bit の加算がしたくなってきます。4 bit などの固定長としても良いですが、我々が今利用しているのはソフトウェアですので、ビット長くらいパラメトリックにしたいものです。C++には可変長テンプレートという N bit 加算器のための機能がありますので、こちらを利用して実装してみます。

バイナリ型シーケンスの作成

N bit の加算器を作成するにあたっては、その加算対象となる値や得られる結果をバイナリ型のシーケンスとして扱いたくなります。型のシーケンスなんて作れるのかと思うかもしれませんが、それほど難しくありません。以下をbinary.hに追記します。

binary.h

    template <typename T>
    struct IType {
        using type = T;
    };

    template <IsBinary... Bs>
    struct BinarySeq;

    template<typename IndexSeq, IsBinary SetType, std::size_t Pos, std::size_t Len, IsBinary... Ts>
    struct BinarySeqSetHelper;

    template<std::size_t... Indexes, IsBinary SetType, std::size_t Pos, std::size_t Len, IsBinary... Ts>
    struct BinarySeqSetHelper<std::index_sequence<Indexes...>, SetType, Pos, Len, Ts...>
      : IType<BinarySeq<
            std::tuple_element_t<Indexes == Pos ? Len : Indexes, std::tuple<Ts..., SetType>>...>> {
        static_assert(Pos < Len, "out of range");
    };

    template<IsBinary... Bs>
    struct BinarySeq : IType<BinarySeq<Bs...>> {
        static constexpr const std::size_t size = sizeof...(Bs);

        template<IsBinary SetType, std::size_t Pos>
        using Set = typename BinarySeqSetHelper<std::make_index_sequence<sizeof...(Bs)>,
                                 SetType,
                                 Pos,
                                 sizeof...(Bs),
                                 Bs...>::type;
    };

    template<IsBinary B, std::size_t N, IsBinary... Bs>
    struct GenBinarySeq {
        using type = typename GenBinarySeq<B, N - 1, Bs..., B>::type;
    };

    template<IsBinary B, IsBinary... Bs>
    struct GenBinarySeq<B, 0, Bs...> {
        using type = typename IType<BinarySeq<Bs...>>::type;
    };

ここでは、BinarySeqという可変長テンプレートパラメータに IsBinary を満たすバイナリ型を持つ型を定義しています。BinarySeqが持つ型パラメータを型シーケンスと見做すわけです。BinarySeqにはSetという型エイリアステンプレートが含まれていますが、このSetはテンプレートパラメータとしてシーケンス上の位置と書き込みたい型を指定すると、そのように編集した後の型シーケンスを表すようになるという機能を持っています。また、GenBinarySeqという型も定義されています。これは、テンプレートパラメータとして型と長さを指定すると、指定された型と長さを持つBinarySeqを作成してくれます。

`BinarySeq`を出力可能にする

バイナリ型を任意の長さのシーケンスとして保持できるようになったのは良いですが、これは値ではなく型テンプレートパラメータとして保持されているに過ぎません。これを我々の確認できる形で出力することは、以下のような実装で実現することが出来ます。

BinarySeqの出力実装

template <typename Bs>
struct BinarySeqPrintHelper;

template <Binary::IsBinary... S>
struct BinarySeqPrintHelper<Binary::BinarySeq<S...>> {
    static void print() {
        (fmt::print("{}", bitToCharV<S>), ...);
    }
};

テンプレートの部分特殊化を利用して、BinarySeqの型パラメータ部分だけを取り出し、c++17 で導入された fold expression で出力しています。

`BinarySeq`を使ってみる

言葉で言われてもわかりにくいかと思いますので、実際のBinarySeqの動作を示すサンプルを提示します。

BinarySeqのサンプルコード

int main()
{
    using Seq1 = Binary::BinarySeq<I, I, I, O, O, I, O, I>;
    fmt::print("1: ");
    BinarySeqPrintHelper<Seq1>::print();
    fmt::print("\n");

    using Seq2 = Seq1::Set<I, 4>::Set<O, 1>;
    fmt::print("2: ");
    BinarySeqPrintHelper<Seq2>::print();
    fmt::print("\n");

    using Seq3 = Binary::GenBinarySeq<O, 4>::type;
    fmt::print("3: ");
    BinarySeqPrintHelper<Seq3>::print();
    fmt::print("\n");

    using Seq4 = Binary::GenBinarySeq<I, 5>::type;
    fmt::print("4: ");
    BinarySeqPrintHelper<Seq4>::print();
    fmt::print("\n");

    using Seq5 = Seq3::Set<I, 2>;
    fmt::print("5: ");
    BinarySeqPrintHelper<Seq5>::print();
    fmt::print("\n");
}

1: 11100101
2: 10101101
3: 0000
4: 11111
5: 0010

完全に型テンプレートパラメータが「任意長で扱えて」、「要素の編集も可能」なリストと化しています。きっとそういう機能なんだと思います(？)。

N bit 加算器本体

ここまでで、すべての準備は整いました。あとはこれらを利用して N bit 加算器を実装するだけです。もったいぶっても仕方ないので(小出しにして詳細に説明するのが面倒なので)実装を貼ります。

n_bit_adder.h

#pragma once

#include <tuple>
#include "basic_adders.h"

namespace Circuits {
    template <std::size_t Len, typename BS1, typename BS2, typename BS3, Binary::IsBinary Ci>
    struct NbitAdderHelper;

    template <Binary::IsBinary... S1, Binary::IsBinary... S2, Binary::IsBinary... S3, Binary::IsBinary Ci>
    struct NbitAdderHelper<sizeof...(S1), Binary::BinarySeq<S1...>, Binary::BinarySeq<S2...>, Binary::BinarySeq<S3...>, Ci> {
        static_assert(sizeof...(S1) == sizeof...(S2) && sizeof...(S1) == sizeof...(S3), "Bit length not matched.");
        static constexpr const std::size_t N = sizeof...(S1);
        using A = std::tuple_element_t<N-1, std::tuple<S1...>>;
        using B = std::tuple_element_t<N-1, std::tuple<S2...>>;
        using HAdder = Circuits::HalfAdder<A, B>;

        using Ss = typename NbitAdderHelper<N-1, Binary::BinarySeq<S1...>, Binary::BinarySeq<S2...>, typename Binary::BinarySeq<S3...>::template Set<typename HAdder::X, N-1>, typename HAdder::Y>::Ss;
    };

    template <std::size_t N, Binary::IsBinary... S1, Binary::IsBinary... S2, Binary::IsBinary... S3, Binary::IsBinary Ci>
    struct NbitAdderHelper<N, Binary::BinarySeq<S1...>, Binary::BinarySeq<S2...>, Binary::BinarySeq<S3...>, Ci> {
        static_assert(sizeof...(S1) == sizeof...(S2) && sizeof...(S1) == sizeof...(S3), "Bit length not matched.");
        using A = std::tuple_element_t<N-1, std::tuple<S1...>>;
        using B = std::tuple_element_t<N-1, std::tuple<S2...>>;
        using FAdder = Circuits::FullAdder<A, B, Ci>;

        using Ss = typename NbitAdderHelper<N-1, Binary::BinarySeq<S1...>, Binary::BinarySeq<S2...>, typename Binary::BinarySeq<S3...>::template Set<typename FAdder::X, N-1>, typename FAdder::Y>::Ss;
    };

    template <Binary::IsBinary... S1, Binary::IsBinary... S2, Binary::IsBinary... S3, Binary::IsBinary Ci>
    struct NbitAdderHelper<0, Binary::BinarySeq<S1...>, Binary::BinarySeq<S2...>, Binary::BinarySeq<S3...>, Ci> {
        static_assert(sizeof...(S1) == sizeof...(S2) && sizeof...(S1) == sizeof...(S3), "Bit length not matched.");
        using Ss = Binary::BinarySeq<Ci, S3...>;
    };

    template <typename BS1, typename BS2>
    using NbitAdder = NbitAdderHelper<BS1::size, BS1, BS2, typename Binary::GenBinarySeq<Binary::O, BS1::size>::type, Binary::O>;
}

いや～ C++は良い言語ですね！！！！このコードでやっているのは、先に示した回路図の安直な再現です。「一番はじめの半加算器」「2 番目～から[ビット長-1]番目の全加算器」「終了処理」の 3 つに特殊化されるように実装を切り分け、再帰的に演算結果を伝達させていっています。テンプレートパラメータの名前で説明するのならば、「std::size_t Nがその時に対象としている半加算器/全加算器の通番」「typename BS1とtypename BS2は加算に使われる 2 つのバイナリ型シーケンス」「typename BS3は演算結果を保持しているバイナリ型シーケンス」「Binary::IsBinary Ciは下位の加算器からの桁上り入力」です。結果として、演算対象とするシーケンスを受け取ったNbitAdderHelper型は「先頭に最後の桁上り、2 番めから終端までが演算結果」となるバイナリ型シーケンスを示す型Ssを内部に持つようになります。読みにくさはピカイチですが、やっていることはそんなに複雑ではありません。

この実装では与えられるBinarySeqの長さが同一でなければ静的アサートでコンパイルエラーとなるようにしています。しかし、今回の処理は加算であるため、単純な 0 埋めの(メタ)実装を追加することで異なる長さのBinarySeqも加算可能になります(あれ、でもそれって加算回路的にどうなの)。

ここで例によって、結果を見える形にするための出力処理を実装しておきます。

NbitAdderprintHelper

template <typename Bs>
struct NbitAdderPrintHelper;

template <Binary::IsBinary... S1, Binary::IsBinary... S2>
struct NbitAdderPrintHelper<Circuits::NbitAdder<Binary::BinarySeq<S1...>, Binary::BinarySeq<S2...>>> {
    static void print_result() {
        (fmt::print("{}", bitToCharV<S1>), ...);
        fmt::print(" + ");
        (fmt::print("{}", bitToCharV<S2>), ...);

        using Adder = Circuits::NbitAdder<Binary::BinarySeq<S1...>, Binary::BinarySeq<S2...>>;
        fmt::print(" = ");
        BinarySeqPrintHelper<typename Adder::Ss>::print();
        fmt::print("\n");
    }
};

特筆すべきところは特にありませんね。では結果を確認していきましょう！

Nbit加算器動作確認

int main()
{
    using ASeq = Binary::BinarySeq<I, I, I, O, O, I, O, I, O, O, I, I, O, I, I, O>;
    using BSeq = Binary::BinarySeq<I, I, O, I, O, O, I, I, O, I, O, O, O, O, I, I>;
    NbitAdderPrintHelper<Circuits::NbitAdder<ASeq, BSeq>>::print_result();
}

1110010100110110 + 1101001101000011 = 11011100001111001

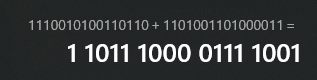
この結果が正しいのか、Windows の電卓くんに計算してもらいました。出力検証結果

やった！完璧ですね！！C++の型システム上で N bit の加算器を動作させることに成功しました！！

おわりに

ここまで記事を読んでくださった方に朗報があります。C++には**+演算子**と呼ばれる演算子が存在しており、以下のように記述することで加算を行うことが出来ます。

add

1 + 2 // → 3

また、このようにコンパイル時に値が確定するリテラルとして表記された値は、コンパイラの最適化によってコンパイル時に演算結果の値へと置き換えられることが殆どであり、実行時コストを考える必要もありません。2 進数以外読めないという方も安心してください。C++14 からの C++は 2 進数リテラルを持っています。

bin_add

0b1 + 0b10 // → 0b11 (3)

よって、C++の型システムで加算器を実装する必要はありません。

追記

本記事で利用したソースコードを GitHub にあげておきました。 https://github.com/strvworks/logical_cpp/tree/master

レギュレーション

検証環境

注意点

バイナリ型を定義する

最低限の出力処理を用意しておく

基本論理ゲートを実装する

NAND ゲート型

その他のゲートの型を用意する

基本論理ゲートのソースコード

加算器

半加算器

全加算器

N bit 加算器

バイナリ型シーケンスの作成

BinarySeqを出力可能にする

BinarySeqを使ってみる

N bit 加算器本体

おわりに

追記

share

`BinarySeq`を出力可能にする

`BinarySeq`を使ってみる